Casing Weights and Grades
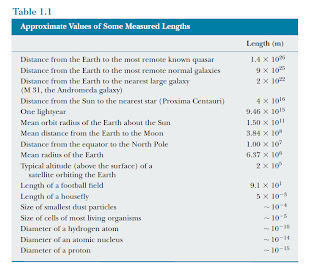
Common casing diameters range from less than 4-1/2 in. to over 20 in., and common tubing sizes are from 3/4 in. to over 4-1/2 in. In some high rate wells, tubing may be 5-1/2 in. to over 7 in. and 2-7/8 in. casing is run in tubingless completions. After the size is determined, the grade of the steel must be selected. The grades, along with weight, are based on pressure and corrosion requirements. The grades of steel used in oil industry tubularsare shown in the following table for API and non-API sizes. The letters are assigned only to avoid confusion. Grades N-80 and stronger are considered high strength steels. Use of the higher strength steels increases cost and decreases resistance to some forms of corrosion. Use of the very hardalloys, such as V-150, makes packer setting difficult since the slips have difficulty setting in the very hard steel of the casing.
The yield and burst strength values for each casing size and weight are available from detailed tables are used for selection of casing once the necessary strength calculations are made. Often, because of economics or efforts to lighten the casing string, lower grade or lighter weight casing may be considered. Because the weight and pressure loads on a casing string change from top to bottom, a well designed string may incorporate several weights and grades of casing.
Casing Design Safety Factors
tension 1.6 to 1.8
burst 1.25 to 1.30
collapse 1 .O to 1.25
Earth shift forces, such as salt movement or other faulting and folding events caused by tectonic movement or are very difficult to address with a traditional safety factor. These forces have been successfully offset in some cases by designs using very heavy wall pipe or concentric pipe (casing cemented inside casing) over the affected zone. These types of casing designs are rare and most are generated by a series of trail and error approaches.
Load Description
The casing string must be designed for any load encountered from mud or reservoir fluids in placement or during any phase of stimulation or production. The common forces are tension during running, internal pressures during drilling, completion or production, and external pressures caused by drawdown, mechanical loads, and zone pressures. These loads are tension, burst, and collapse. The loads are often applied simultaneously in different parts of the string, and the forces may interact. The tension design of the casing string is made as if it were hanging free in air. A safety factor of 1.6 to 1.8 is applied to make allowances for a number of other tension factor^.^*^^'' These factors are briefly discussed in the following paragraphs. Collapse, burst, and tension forces are explained separately, but all must be satisfactorily accounted for in the final design. The design methods in this book result in a conservative design. Each design method is based on the worst possible case that could
occur during running. Collapse loading is force applied from outside the casing by either fluid pressure in a zone or earth shift forces. Forces from fluid pressure are collapse loadings while earth shift forces produce mechanical crush loadings. The largest collapse load from fluid pressure will usually be exhibited at the bottom of the string where hydrostatic pressure is greatest. The exception is an isolated, very high pressure zone. These zones are usually noted on the drilling record as places where kicks are taken.
The occurrence of earth shift zones from faults or salt movement are much harder to locate, especially on wildcats but may often show up on the drilling record as sticking points (not associated with mud cake buildup) or zones that have to be reamed or redrilled to get back to gauge hole size. The occurrence of salt zones are a very important tip to potential casing problem^.^ In one study area, 87% of the wells around a salt dome suffered some casing diameter reduction due to external, earth shift force.
’In the collapse design for fluid pressure, the worst case loading occurs with the unlikely combination of an empty casing string in a hole full of mud. A proper design, for effects of collapse only, would be a casing string that is strongest at the bottom and weakest at the top. Collapse is also affected by the effects of tension, which reduces the collapse rating or the “set depth limit” of the casing. As an object is pulled, it is more likely to lose diameter as it stretches in length. This thinning is a force in the same direction as collapse forces. Fortunately, the point at which the effect of tension induced “narrowing” of the string is at maximum is at the surface where effects of collapse pressure from hydrostatic pressure are the lowest. Burst pressure is a force applied from inside the casing by produced fluid pressures, hydrostatic mud load or addition of surface pressure during stimulation or workover operations. Since there is usually mud hydrostatic pressure along the outside of the casing before and during cementing, the net pressure or the difference between the pressure inside the casing and outside the casing will be used in the design of the casing. Unlike collapse, however, the shallower casing section is also important in the burst calculations from a safety standpoint. Burst pressures exerted by produced fluids are maximum at the surface (no offsetting hydrostatic load), while those exerted by mud is maximum at the bottom of the well. During fracturing, high burst loads may be exerted all along the string. Because collapse loads offset the burst load at the bottom of the string, the burst calculation is usually important above the “buoyancy neutral point.” This will be developed later. Tension is a force produced by the weight of the casing, the pressure differential, and the mud weights inside and outside the casing. It is largest at the top of the string and decreases with depth toward the bottom of the string. The tension load is partially offset by the buoyancy of the string in mud and is affected by pressure. When the pressure inside the tube rises, the pipe diameter is expanded and the length shortened or the tension is increased in a pipe that is anchored to prevent upward movement. When the pressure outside of a tube rises, the tube is elongated or the compression is increased if the
ends are fixed, Figure 2.6. Buckling failure in casing usually results from axial compression (lengthwise) overloading. The load produces ridges in the casing walls or corkscrewing of the tube. Either of these actions relieve compression, but the pipe is usually permanently yielded. The effects of buckling, Figure 2.7, is critical on the design of the casing string. The neutral point, Figure 2.8, is the dividing line between where buckling may occur and where it cannot occur in a tube that is evenly loaded around its radius. Above the neutral point, the tube is in tension and will not buckle. Below the neutral point, the upward buoyancy of the mud and other forces including pressure and mechanical loading place the tube in compression. Buckling can occur if the compressive load is more than the pipe can tolerate in the wellbore surroundings. The following information describes the neutral point, first in a theoretical manner and then in a practical way. There can be a neutral point in the casing or tubing string described by the formula:’*
When F, is algebraically greater than the right-hanc side of the equation, the pipe tends to be straldht. When F, is less than the equation, the pipe tends to buckle. When F, is equal to the equation, the neutral point is reached. The right-hand side of Eqn. (2.1) may also be referred to as the stability force. The true axial force will vary from point to point in the string, and will also vary over the life of the well. Typical considerations necessary to compute F, include the conditions at the time of cementing the casing or setting the packer in the case of tubing, as well as changes in the environment (temperature and pressure) to which the tubular is exposed. For casing, buckling primarily affects wear, particularly for intermediate strings through which additional drilling will occur. In extreme cases, splitting may
also be common. For tubing, the radial clearance between tubing and casing is usually sufficient to allow corkscrewing, often producing permanent deformation of the buckled portion of the string.
This equation is only appropriate for an open ended tube, clamped at both ends, with PO = 0 and AT = 0 , and ignoring weight. Under the unlikely conditions of a weightless string with no outside pressure, buckling in tension is possible. To illustrate the impact of Eqn. 2.2, consider a weightless tube that is open ended and subject to internal pressure only. For this loading, the only axial force is that due to ballooning given by Eqn. 2.2 and shown previously in Figure 2.6. As the inside pressure is increased, F, increases as 2pPjAis but the right hand side of Eqn. 2.1 increases as PjAi. The tube will not only buckle immediately, but will also buckle in tension.
Each zone or section of the casing string is checked for tensile requirements following collapse and burst calculations. In case of corrections made to a string design to compensate for tension load requirements, the order of selection is usually: (1) stronger connection, (2) higher grade (stronger steel), and (3) higher weight. Increasing connection strength and steel grade is preferred since they increase total string strength without adding significant weight. There are so many “premium” connections available that it is difficult to present a comprehensive data set. Tables of connection specifics are published yearly.37
For the sole purpose of casing collapse strength derating due to the effects of tension, a practical “buoyancy neutral point”, designated N.P., can be estimated by Eqn. (2.4) where:
The collapse resistance values given in the manufacturer tables are for casing that is not affected by axial load. In a well, the casing will be stressed by fluid pressures, Figure 2.9, mechanical bending forces, Figure 2.10, and tensile forces produced by the hanging weight of the casing. In collapse calculations, axial tension produces a reduction in collapse resistance. For purposes of this example, the axial tension is assumed to be from tension loads on a straight, free hanging pipe and not from bending loads.
Designing for forces involving earth shifts, highly deviated hole, sticking, reciprocating and rotating casing while cementing or running stresses, involves field optimization and the criteria for design differ from company to company. Earth shift design usually involves multiple strings of pipe or very heavy wall pipe across the problem zone. Problem zone recognition can often be made from drilling records where bit dragging (nonassociated with mud cake buildup) occurs long after a zone is drilled. Wells near salt domes or flows are considered likely prospects for formation movement.