Although there are many different geophysical methods, small-scale surveys
all tend to be rather alike and involve similar, and sometimes ambiguous,
jargon. For example, the word base has three different common meanings,
and stacked and field have two each.
Measurements in geophysical surveys are made in the field but, unfortunately,
many are also of fields. Field theory is fundamental to gravity,
magnetic and electromagnetic work, and even particle fluxes and seismic
wavefronts can be described in terms of radiation fields. Sometimes ambiguity
is unimportant, and sometimes both meanings are appropriate (and
intended), but there are occasions when it is necessary to make clear distinctions.
In particular, the term field reading is almost always used to identify
readings made in the field, i.e. not at a base station.
The fields used in geophysical surveys may be natural ones (e.g. the
Earth’s magnetic or gravity fields) but may be created artificially, as when
alternating currents are used to generate electromagnetic fields. This leads to
the broad classification of geophysical methods into passive and active types,
respectively.
Physical fields can be illustrated by lines of force that show the field
direction at any point. Intensity can also be indicated, by using more closely
spaced lines for strong fields, but it is difficult to do this quantitatively where
three-dimensional situations are being illustrated on two-dimensional media.
Vector addition
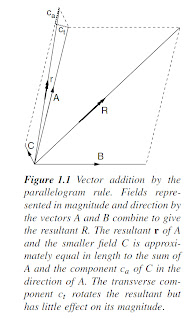
Vector addition (Figure 1.1) must be used when combining fields from different
sources. In passive methods, knowledge of the principles of vector
addition is needed to understand the ways in which measurements of local
anomalies are affected by regional backgrounds. In active methods, a local
anomaly (secondary field) is often superimposed on a primary field produced
by a transmitter. In either case, if the local field is much the weaker of the two
(in practice, less than one-tenth the strength of the primary or background
field), then the measurement will, to a first approximation, be made in the
direction of the stronger field and only the component in this direction of
the secondary field (ca in Figure 1.1) will be measured. In most surveys the
slight difference in direction between the resultant and the background or
primary field can be ignored.
If the two fields are similar in
strength, there will be no simple
relationship between the magnitude
of the anomalous field and the
magnitude of the observed anomaly.
However, variations in any given
component of the secondary field
can be estimated by taking all
measurements in an appropriate
direction and assuming that the
component of the background or
primary field in this direction is
constant over the survey area.
Measurements of vertical rather than
total fields are sometimes preferred
in magnetic and electromagnetic
surveys for this reason.
The fields due to multiple sources
are not necessarily equal to the
vector sums of the fields that would
have existed had those sources
been present in isolation. A strong
magnetic field from one body can
affect the magnetization in another,
or even in itself (demagnetization
effect), and the interactions between fields and currents in electrical and
electromagnetic surveys can be very complex.
The inverse-square law
Inverse-square law attenuation of signal strength occurs in most branches of
applied geophysics. It is at its simplest in gravity work, where the field due
to a point mass is inversely proportional to the square of the distance from
the mass, and the constant of proportionality (the gravitational constant G)
is invariant. Magnetic fields also obey an inverse-square law. The fact that
their strength is, in principle, modified by the permeability of the medium
is irrelevant in most geophysical work, where measurements are made in
either air or water. Magnetic sources are, however, essentially bipolar, and
the modifications to the simple inverse-square law due to this fact are much
more important (Section 1.1.5).
Electric current flowing from an isolated point electrode embedded in
a continuous homogeneous ground provides a physical illustration of the
significance of the inverse-square law. All of the current leaving the electrode
must cross any closed surface that surrounds it. If this surface is a sphere
concentric with the electrode, the same fraction of the total current will cross
each unit area on the surface of the sphere. The current per unit area will
therefore be inversely proportional to the total surface area, which is in turn
proportional to the square of the radius. Current flow in the real Earth is, of
course, drastically modified by conductivity variations.
1.1.3 Two-dimensional sources
Rates of decrease in field strengths depend on source shapes as well as on
the inverse-square law. Infinitely long sources of constant cross-section are
termed two-dimensional (2D) and are often used in computer modelling to
approximate bodies of large strike extent. If the source ‘point’ in Figure 1.2
represents an infinite line source seen end on, the area of the enclosing (cylindrical)
surface is proportional to the radius. The argument applied in the
previous section to a point source implies that in this case the field strength
is inversely proportional to distance and not to its square. In 2D situations,
lines of force drawn on pieces of paper illustrate field magnitude (by their
separation) as well as direction.
The lines of force or radiation intensity from a source consisting of a homogeneous layer of
constant thickness diverge only near its edges (Figure 1.3). The Bouguer plate of gravity reductions (Section 2.5.1) and the radioactive source with 2π geometry (Section 4.3.3) are examples of infinitely extended layer sources, for which field strengths are independent
of distance. This condition is approximately achieved if a detector is only a short distance
above an extended source and a long way from its edges.
A dipole consists of equal-strength positive and negative point sources a very small distance apart. Field strength decreases as the inverse cube of distance and both strength and direction change with ‘latitude’ (Figure 1.4). The intensity of the field at a point on a dipole
axis is double the intensity at a point the same distance away on the dipole ‘equator’, and in the opposite direction.
Electrodes are used in some
electrical surveys in approximately
dipolar pairs and magnetization is
fundamentally dipolar. Electric currents
circulating in small loops are
dipolar sources of magnetic field.
Exponential decay
Radioactive particle fluxes and seismic and electromagnetic waves are subject
to absorption as well as geometrical attenuation, and the energy crossing
closed surfaces is then less than the energy emitted by the sources they
enclose. In homogeneous media, the percentage loss of signal is determined
by the path length and the attenuation constant. The absolute loss is proportional
also to the signal strength. A similar exponential law (Figure 1.5),
governed by a decay constant, determines the rate of loss of mass by a
radioactive substance.
Attenuation rates are alternatively characterized by skin depths, which
are the reciprocals of attenuation constants. For each skin depth travelled, the
signal strength decreases to 1/e of its original value, where e (= 2.718) is the
base of natural logarithms. Radioactivity decay rates are normally described in
terms of the half-lives, equal to loge2 (= 0.693) divided by the decay constant.
During each half-life period, one half of the material present at its start is lost.
all tend to be rather alike and involve similar, and sometimes ambiguous,
jargon. For example, the word base has three different common meanings,
and stacked and field have two each.
Measurements in geophysical surveys are made in the field but, unfortunately,
many are also of fields. Field theory is fundamental to gravity,
magnetic and electromagnetic work, and even particle fluxes and seismic
wavefronts can be described in terms of radiation fields. Sometimes ambiguity
is unimportant, and sometimes both meanings are appropriate (and
intended), but there are occasions when it is necessary to make clear distinctions.
In particular, the term field reading is almost always used to identify
readings made in the field, i.e. not at a base station.
The fields used in geophysical surveys may be natural ones (e.g. the
Earth’s magnetic or gravity fields) but may be created artificially, as when
alternating currents are used to generate electromagnetic fields. This leads to
the broad classification of geophysical methods into passive and active types,
respectively.
Physical fields can be illustrated by lines of force that show the field
direction at any point. Intensity can also be indicated, by using more closely
spaced lines for strong fields, but it is difficult to do this quantitatively where
three-dimensional situations are being illustrated on two-dimensional media.
Vector addition
Vector addition (Figure 1.1) must be used when combining fields from different
sources. In passive methods, knowledge of the principles of vector
addition is needed to understand the ways in which measurements of local
anomalies are affected by regional backgrounds. In active methods, a local
anomaly (secondary field) is often superimposed on a primary field produced
by a transmitter. In either case, if the local field is much the weaker of the two
(in practice, less than one-tenth the strength of the primary or background
field), then the measurement will, to a first approximation, be made in the
direction of the stronger field and only the component in this direction of
the secondary field (ca in Figure 1.1) will be measured. In most surveys the
slight difference in direction between the resultant and the background or
primary field can be ignored.
If the two fields are similar in
strength, there will be no simple
relationship between the magnitude
of the anomalous field and the
magnitude of the observed anomaly.
However, variations in any given
component of the secondary field
can be estimated by taking all
measurements in an appropriate
direction and assuming that the
component of the background or
primary field in this direction is
constant over the survey area.
Measurements of vertical rather than
total fields are sometimes preferred
in magnetic and electromagnetic
surveys for this reason.
The fields due to multiple sources
are not necessarily equal to the
vector sums of the fields that would
have existed had those sources
been present in isolation. A strong
magnetic field from one body can
affect the magnetization in another,
or even in itself (demagnetization
effect), and the interactions between fields and currents in electrical and
electromagnetic surveys can be very complex.
The inverse-square law
Inverse-square law attenuation of signal strength occurs in most branches of
applied geophysics. It is at its simplest in gravity work, where the field due
to a point mass is inversely proportional to the square of the distance from
the mass, and the constant of proportionality (the gravitational constant G)
is invariant. Magnetic fields also obey an inverse-square law. The fact that
their strength is, in principle, modified by the permeability of the medium
is irrelevant in most geophysical work, where measurements are made in
either air or water. Magnetic sources are, however, essentially bipolar, and
the modifications to the simple inverse-square law due to this fact are much
more important (Section 1.1.5).
Electric current flowing from an isolated point electrode embedded in
a continuous homogeneous ground provides a physical illustration of the
significance of the inverse-square law. All of the current leaving the electrode
must cross any closed surface that surrounds it. If this surface is a sphere
concentric with the electrode, the same fraction of the total current will cross
each unit area on the surface of the sphere. The current per unit area will
therefore be inversely proportional to the total surface area, which is in turn
proportional to the square of the radius. Current flow in the real Earth is, of
course, drastically modified by conductivity variations.
1.1.3 Two-dimensional sources
Rates of decrease in field strengths depend on source shapes as well as on
the inverse-square law. Infinitely long sources of constant cross-section are
termed two-dimensional (2D) and are often used in computer modelling to
approximate bodies of large strike extent. If the source ‘point’ in Figure 1.2
represents an infinite line source seen end on, the area of the enclosing (cylindrical)
surface is proportional to the radius. The argument applied in the
previous section to a point source implies that in this case the field strength
is inversely proportional to distance and not to its square. In 2D situations,
lines of force drawn on pieces of paper illustrate field magnitude (by their
separation) as well as direction.
The lines of force or radiation intensity from a source consisting of a homogeneous layer of
constant thickness diverge only near its edges (Figure 1.3). The Bouguer plate of gravity reductions (Section 2.5.1) and the radioactive source with 2π geometry (Section 4.3.3) are examples of infinitely extended layer sources, for which field strengths are independent
of distance. This condition is approximately achieved if a detector is only a short distance
above an extended source and a long way from its edges.
A dipole consists of equal-strength positive and negative point sources a very small distance apart. Field strength decreases as the inverse cube of distance and both strength and direction change with ‘latitude’ (Figure 1.4). The intensity of the field at a point on a dipole
axis is double the intensity at a point the same distance away on the dipole ‘equator’, and in the opposite direction.
Electrodes are used in some
electrical surveys in approximately
dipolar pairs and magnetization is
fundamentally dipolar. Electric currents
circulating in small loops are
dipolar sources of magnetic field.
Exponential decay
Radioactive particle fluxes and seismic and electromagnetic waves are subject
to absorption as well as geometrical attenuation, and the energy crossing
closed surfaces is then less than the energy emitted by the sources they
enclose. In homogeneous media, the percentage loss of signal is determined
by the path length and the attenuation constant. The absolute loss is proportional
also to the signal strength. A similar exponential law (Figure 1.5),
governed by a decay constant, determines the rate of loss of mass by a
radioactive substance.
Attenuation rates are alternatively characterized by skin depths, which
are the reciprocals of attenuation constants. For each skin depth travelled, the
signal strength decreases to 1/e of its original value, where e (= 2.718) is the
base of natural logarithms. Radioactivity decay rates are normally described in
terms of the half-lives, equal to loge2 (= 0.693) divided by the decay constant.
During each half-life period, one half of the material present at its start is lost.