Like all other sciences, physics is based on experimental observations and quantitative measurements. The main objective of physics is to find the limited number of fundamental
laws that govern natural phenomena and to use them to develop theories that can predict the results of future experiments. The fundamental laws used in developing theories are expressed in the language of mathematics, the tool that provides a bridge between theory and experiment. When a discrepancy between theory and experiment arises, new theories must be formulated to remove the discrepancy. Many times a theory is satisfactory only under limited conditions; a more general theory might be satisfactory without such limitations. For example, the laws of motion discovered by Isaac Newton (1642–1727) in the
17th century accurately describe the motion of objects moving at normal speeds but do
not apply to objects moving at speeds comparable with the speed of light. In contrast,
the special theory of relativity developed by Albert Einstein (1879–1955) in the early 1900s gives the same results as Newton’s laws at low speeds but also correctly describes
motion at speeds approaching the speed of light. Hence, Einstein’s special theory of
relativity is a more general theory of motion. Classical physics includes the theories, concepts, laws, and experiments in classical mechanics, thermodynamics, optics, and electromagnetism developed before 1900. Important contributions to classical physics were provided by Newton, who developed classical mechanics as a systematic theory and was one of the originators of calculus as a mathematical tool. Major developments in mechanics continued in the 18th century, but the fields of thermodynamics and electricity and magnetism were not developed until the latter part of the 19th century, principally because before that time the apparatus for controlled experiments was either too crude or unavailable. A major revolution in physics, usually referred to as modern physics, began near the end of the 19th century. Modern physics developed mainly because of the discovery that many physical phenomena could not be explained by classical physics. The two most important developments in this modern era were the theories of relativity and quantum mechanics. Einstein’s theory of relativity not only correctly described the motion of objects moving at speeds comparable to the speed of light but also completely revolutionized the traditional concepts of space, time, and energy. The theory of relativity also shows that the speed of light is the upper limit of the speed of an object and that mass
and energy are related. Quantum mechanics was formulated by a number of distinguished
scientists to provide descriptions of physical phenomena at the atomic level. Scientists continually work at improving our understanding of fundamental laws, and new discoveries are made every day. In many research areas there is a great deal of overlap among physics, chemistry, and biology. Evidence for this overlap is seen in the names of some subspecialties in science—biophysics, biochemistry, chemical physics, biotechnology, and so on. Numerous technological advances in recent times are the result of the efforts of many scientists, engineers, and technicians. Some of the most notable developments in the latter half of the 20th century were
(1) unmanned planetary explorations and manned moon landings,
(2) microcircuitry and high-speed computers,
(3) sophisticated imaging techniques used in scientific research and medicine, and
(4) several remarkable results in genetic engineering. The impacts of such developments
and discoveries on our society have indeed been great, and it is very likely that
future discoveries and developments will be exciting, challenging, and of great benefit
to humanity.
1.1 Standards of Length, Mass, and Time
The laws of physics are expressed as mathematical relationships among physical quantities
that we will introduce and discuss throughout the book. Most of these quantities are derived quantities, in that they can be expressed as combinations of a small number of basic quantities. In mechanics, the three basic quantities are length, mass, and time. All other quantities in mechanics can be expressed in terms of these three. If we are to report the results of a measurement to someone who wishes to reproduce this measurement, a standard must be defined. It would be meaningless if a visitor from another planet were to talk to us about a length of 8 “glitches” if we do not know the meaning of the unit glitch. On the other hand, if someone familiar with our system of measurement reports that a wall is 2 meters high and our unit of length is defined to be 1 meter, we know that the height of the wall is twice our basic length unit. Likewise, if we are told that a person has a mass of 75 kilograms and our unit of mass is defined to be 1 kilogram, then that person is 75 times as massive as our basic unit.1 Whatever is chosen as a standard must be readily accessible and possess some property that can be measured reliably. Measurements taken by different people in different places must yield the same result. In 1960, an international committee established a set of standards for the fundamental quantities of science. It is called the SI (Système International), and its units of length, mass, and time are the meter, kilogram, and second, respectively. Other SI standards established by the committee are those for temperature (the kelvin), electric current (the ampere), luminous intensity (the candela), and the amount of substance (the mole).
that we will introduce and discuss throughout the book. Most of these quantities are derived quantities, in that they can be expressed as combinations of a small number of basic quantities. In mechanics, the three basic quantities are length, mass, and time. All other quantities in mechanics can be expressed in terms of these three. If we are to report the results of a measurement to someone who wishes to reproduce this measurement, a standard must be defined. It would be meaningless if a visitor from another planet were to talk to us about a length of 8 “glitches” if we do not know the meaning of the unit glitch. On the other hand, if someone familiar with our system of measurement reports that a wall is 2 meters high and our unit of length is defined to be 1 meter, we know that the height of the wall is twice our basic length unit. Likewise, if we are told that a person has a mass of 75 kilograms and our unit of mass is defined to be 1 kilogram, then that person is 75 times as massive as our basic unit.1 Whatever is chosen as a standard must be readily accessible and possess some property that can be measured reliably. Measurements taken by different people in different places must yield the same result. In 1960, an international committee established a set of standards for the fundamental quantities of science. It is called the SI (Système International), and its units of length, mass, and time are the meter, kilogram, and second, respectively. Other SI standards established by the committee are those for temperature (the kelvin), electric current (the ampere), luminous intensity (the candela), and the amount of substance (the mole).
Length
In A.D. 1120 the king of England decreed that the standard of length in his country
would be named the yard and would be precisely equal to the distance from the tip of
his nose to the end of his outstretched arm. Similarly, the original standard for the foot
adopted by the French was the length of the royal foot of King Louis XIV. This standard
prevailed until 1799, when the legal standard of length in France became the meter,
defined as one ten-millionth the distance from the equator to the North Pole along
one particular longitudinal line that passes through Paris. Many other systems for measuring length have been developed over the years, but the advantages of the French system have caused it to prevail in almost all countries and in scientific circles everywhere. As recently as 1960, the length of the meter was defined as the distance between two lines on a specific platinum–iridium bar stored under controlled conditions in France. This standard was abandoned for several reasons, a principal one being that the limited accuracy with which the separation between the lines on the bar can be determined does not meet the current
requirements of science and technology. In the 1960s and 1970s, the meter was defined
as 1 650 763.73 wavelengths of orange-red light emitted from a krypton-86 lamp. However, in October 1983, the meter (m) was redefined as the distance traveled by light in vacuum during a time of 1/299 792 458 second. In effect, this latest definition establishes that the speed of light in vacuum is precisely 299 792 458
meters per second.
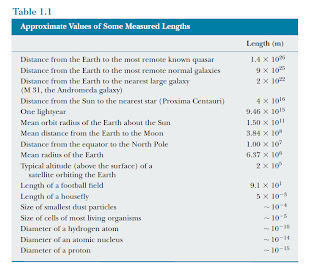
Table 1.1 lists approximate values of some measured lengths. You should study this
table as well as the next two tables and begin to generate an intuition for what is meant
by a length of 20 centimeters, for example, or a mass of 100 kilograms or a time interval
of 3.2 ! 107 seconds.
would be named the yard and would be precisely equal to the distance from the tip of
his nose to the end of his outstretched arm. Similarly, the original standard for the foot
adopted by the French was the length of the royal foot of King Louis XIV. This standard
prevailed until 1799, when the legal standard of length in France became the meter,
defined as one ten-millionth the distance from the equator to the North Pole along
one particular longitudinal line that passes through Paris. Many other systems for measuring length have been developed over the years, but the advantages of the French system have caused it to prevail in almost all countries and in scientific circles everywhere. As recently as 1960, the length of the meter was defined as the distance between two lines on a specific platinum–iridium bar stored under controlled conditions in France. This standard was abandoned for several reasons, a principal one being that the limited accuracy with which the separation between the lines on the bar can be determined does not meet the current
requirements of science and technology. In the 1960s and 1970s, the meter was defined
as 1 650 763.73 wavelengths of orange-red light emitted from a krypton-86 lamp. However, in October 1983, the meter (m) was redefined as the distance traveled by light in vacuum during a time of 1/299 792 458 second. In effect, this latest definition establishes that the speed of light in vacuum is precisely 299 792 458
meters per second.
Table 1.1 lists approximate values of some measured lengths. You should study this
table as well as the next two tables and begin to generate an intuition for what is meant
by a length of 20 centimeters, for example, or a mass of 100 kilograms or a time interval
of 3.2 ! 107 seconds.
Mass
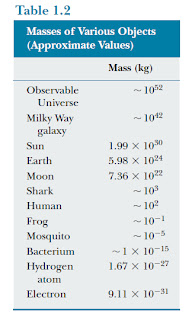
The SI unit of mass, the kilogram (kg), is defined as the mass of a specific platinum–iridium alloy cylinder kept at the International Bureau of Weights and Measures at Sèvres, France. This mass standard was established in 1887 and has not been changed since that time because platinum–iridium is an unusually stable alloy. A duplicate of the Sèvres cylinder is kept at the National Institute of Standards and Technology (NIST) in Gaithersburg, Maryland (Fig. 1.1a). Table 1.2 lists approximate values of the masses of various objects.
Time
Before 1960, the standard of time was defined in terms of the mean solar day for the
year 1900. (A solar day is the time interval between successive appearances of the Sun
at the highest point it reaches in the sky each day.) The second was defined as
of a mean solar day. The rotation of the Earth is now known to vary slightly with time, however, and therefore this motion is not a good one to use for defining a time standard.
In 1967, the second was redefined to take advantage of the high precision attainable
in a device known as an atomic clock (Fig. 1.1b), which uses the characteristic frequency
of the cesium-133 atom as the “reference clock.” The second (s) is now defined as
9 192 631 770 times the period of vibration of radiation from the cesium atom.2
set to them—synchronized, it has sometimes been necessary to add leap seconds to our
clocks.
Since Einstein’s discovery of the linkage between space and time, precise measurement
of time intervals requires that we know both the state of motion of the clock used
to measure the interval and, in some cases, the location of the clock as well. Otherwise,
for example, global positioning system satellites might be unable to pinpoint your location
with sufficient accuracy, should you need to be rescued.
Approximate values of time intervals are presented in Table 1.3.
In addition to SI, another system of units, the U.S. customary system, is still used in the
United States despite acceptance of SI by the rest of the world. In this system, the units of
length, mass, and time are the foot (ft), slug, and second, respectively. In this text we shall
use SI units because they are almost universally accepted in science and industry. We shall
make some limited use of U.S. customary units in the study of classical mechanics.
In addition to the basic SI units of meter, kilogram, and second, we can also use
other units, such as millimeters and nanoseconds, where the prefixes milli- and nanodenote
multipliers of the basic units based on various powers of ten. Prefixes for the
various powers of ten and their abbreviations are listed in Table 1.4. For example,
10"3 m is equivalent to 1 millimeter (mm), and 103 m corresponds to 1 kilometer
(km). Likewise, 1 kilogram (kg) is 103 grams (g), and 1 megavolt (MV) is 106 volts (V).