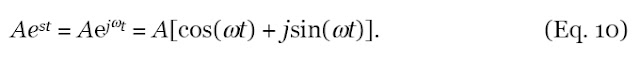Complex Representation of Signals
Most generally, we can use complex or imaginary values for s (and/or A for that matter)
in equation 9, where s is known as the “complex frequency.” In electrical engineering it
is common practice to use the convention that
j = (-1)^.5 in order to avoid confusion with
the use of i to represent current; we will use that convention for the remainder of this
in equation 9, where s is known as the “complex frequency.” In electrical engineering it
is common practice to use the convention that
j = (-1)^.5 in order to avoid confusion with
the use of i to represent current; we will use that convention for the remainder of this
section. When s is purely imaginary, with the value s = jω and A is real, we can take
advantage of Euler’s relation, that:
advantage of Euler’s relation, that:
capacitor. Note that the V is the real part of Aejωt = Re(Aest).
Substituting into equation 8:
We are interested only the real part of the current, of course, so equation 11 simplifies to
iC = –ωCAsin(ωt), the result of equation 6 above. Looking again at equation 9, when
s = jω the ratio of the voltage to the current is 1/ jω C.
Generalization of Ohm’s law
The ratio of a complex voltage, V, to a complex current, I, is represented by the
impedance, Z. Because sinusoidally varying signals are conveniently represented by
complex numbers (and, as we will see when we discuss the Fourier transform in a
separate section, this can be a generalized representation of most any signal we
encounter), this is an exceptionally powerful formalization. For complex signals, Ohm’s
law states simply that:
The magnitude of the impedance is given in units of Ohms, like resistance, but in
general also incorporates a phase shift. For capacitors, as noted above, the impedance is
1/jωC. Applying Voltage as a cosine wave results in a current that is an inverted sine
wave – a 90° phase shift. In general, multiplication by j represents a 90° phase shift.
As we noted above, the voltage and current relationships for most electrical circuits
(specifically, linear electrical circuits), can be found through the application of Ohm’s
law coupled with KVL and KCL. The Laplace transform solution, as in equation 9, allows
this to be generalized readily to the analysis of devices like capacitors, which store
energy.
One should be a little bit careful here concerning the values of ω, which are in units of
radians/second or angular frequency. In common use we generally speak of frequencies
in cycles/second or “Hertz”. As one cycle is 2π radians, ω=2πf, where the letter f denotes
the frequency in cycles/second. When the input voltage is a sinusoid with frequency, f,
equation 9 may be written as:
general also incorporates a phase shift. For capacitors, as noted above, the impedance is
1/jωC. Applying Voltage as a cosine wave results in a current that is an inverted sine
wave – a 90° phase shift. In general, multiplication by j represents a 90° phase shift.
As we noted above, the voltage and current relationships for most electrical circuits
(specifically, linear electrical circuits), can be found through the application of Ohm’s
law coupled with KVL and KCL. The Laplace transform solution, as in equation 9, allows
this to be generalized readily to the analysis of devices like capacitors, which store
energy.
One should be a little bit careful here concerning the values of ω, which are in units of
radians/second or angular frequency. In common use we generally speak of frequencies
in cycles/second or “Hertz”. As one cycle is 2π radians, ω=2πf, where the letter f denotes
the frequency in cycles/second. When the input voltage is a sinusoid with frequency, f,
equation 9 may be written as:
