Kirchhoff’s Laws
The path by which charge may flow between the positive and negative ends of a source
of Voltage or charge is known as a circuit. Sources of current, Voltage, and resistance to
current flow are presented in a set of standard symbols that are connected together in
circuit diagrams. In such diagrams, lines represent perfect, zero resistance, conductors.
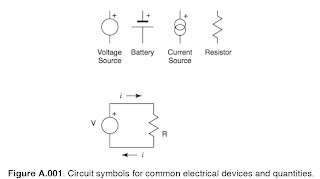
Figure A1.01 shows these standard pictures. By convention, current is said to move from
positive to negative potentials and would imply the motion of positive charges (in
actuality, most currents in man made devices result from the motion of negative
charge). Circuit diagrams frequently use arrows to indicate the direction of current flow.
In the figure, note that the current out from the top, or positive end, of the Voltage
source is identical to the current in to the bottom. The same is true of the resistor in the
circuit and indeed in any element of a circuit: The current flow in is identical to the
current flow out. This general behavior of nodes in a circuit is known as Kirchhoff’s
current law (KCL).
Kirchhoff’s current law has an analog (referred to as a “dual”) in describing Voltage
differences in circuits. Kirchhoff’s Voltage law (KVL) states that the sum of the Voltage
differences around any closed loop in a circuit must be equal to zero. In applying KVL
you must pay attention to the direction you travel in the loop, as discussed below.
Series and Parallel Connections
When electrical elements are attached end-to-end they are connected “in series”, when
the current inputs and outputs of multiple elements are held in common, the devices are
connected in parallel. Figure A1.02 shows resistors connected to a Voltage source in
series and in parallel. In the series circuit, KCL tells us that the current through all three
devices is identical, while KVL informs us that the Voltages V1 and V2 have a sum equal
to Vs. Applying KCL to the parallel circuit we see that at the two nodes, i1 + i2 = i. KVL
tells us that traveling starting at the top and going clockwise around the loop that
includes R1 and R2, V2 – V1 = 0 and that V2 = V1. Likewise, in the loop made up of Vs
and V2, V2 – Vs = 0, implying that V2 = Vs. The two Kirchhoff’s laws, in combination, are
extremely powerful organizing principles. Understanding them makes it possible to
model the behavior of the overwhelming majority of electrical circuits and devices.
law, the voltage across R1 is equal to iR1, and the Voltage that appears across R2 is iR2.
The Voltage that appears across the Voltage source is therefore the sum of the Voltages
across each resistor, or i(R1 + R2) (Note that this is the same as the expression of KVL
for this circuit: Vs = V1 + V2. The total resistance experienced by the Voltage source in
the series circuit is thus the sum of the individual resistors: resistance in series is the
sum of the individual resistances.
In the parallel circuit, there are two paths for current to go through the resistors. Not
surprisingly more current flows through the lower resistance path, and we can compute
the individual currents by Ohm’s law. Because the Voltage (V1 and V2) across these
resistors is identical (they are connected by perfect conductors), the current, i1 in R1 is
V/R1 and i2 is V/R2. By KCL, the total current that flows from the Voltage source is
equal to the sum of the currents through the two resistors:.
